
I(f) (la imagen de f, por abuso de notación) es el conjunto de todos los números enteros no primos de valor absoluto distinto de uno.
El subconjunto I(f)  {1,-1} que, de ahora en adelante llamaremos Z’, goza de las siguientes propiedades:
{1,-1} que, de ahora en adelante llamaremos Z’, goza de las siguientes propiedades:
i) Es cerrado respecto al producto ordinario de los números enteros.
ii) No es cerrado respecto de la suma ordinaria de los números enteros (al respecto, las indeterminaciones son los casos que dan resultados primos).
 {1,-1} que, de ahora en adelante llamaremos Z’, goza de las siguientes propiedades:
{1,-1} que, de ahora en adelante llamaremos Z’, goza de las siguientes propiedades:i) Es cerrado respecto al producto ordinario de los números enteros.
ii) No es cerrado respecto de la suma ordinaria de los números enteros (al respecto, las indeterminaciones son los casos que dan resultados primos).
En este aspecto la estructura es análoga a la del conjunto de los irracionales elementales; este conjunto resulta cerrado respecto del producto y ampliamente abierto con respecto a la suma.
La siguiente tabla muestra una partición del conjunto de los enteros positivos mayores que la unidad. Asociada a esa partición, hay una relación de equivalencia que divide al conjunto en clases. Los representantes mínimos de esas clases son números primos.
Con respecto a este asunto, cito un párrafo de la obra "Análisis Matemático 1", de J. Rey Pastor, P. Pi Calleja y C. A. Trejo, Editorial Kapelusz S. A., Nota 1 al Capítulo 1, parágrafo 1 -6, página 9, decimotercera tirada de la octava edición, febrero de 1985, Bs.As.
"Es importante observar que la relación de equivalencia no nace de la comunidad del carácter abstracto, sino que lo engendra. Por ejemplo. No podemos definir la semejanza como igualdad de forma, pues es justamente la relación de «semejanza» la que permite introducir la noción de «forma». Cada relación de equivalencia permite definir por abstracción un nuevo concepto."
Cuando leí este párrafo, me pregunté ¿cuál es el nuevo concepto que define la relación de equivalencia manifiesta en la tabla? Y si la relación engendra el concepto de número primo, ¿cuál es la relación?
No conozco ninguna técnica para obtener la relación de equivalencia a partir de la partición. Tampoco dieron resultado las consultas que realicé con personas más capacitadas; alguna de ellas manifestó dudas de que ello pudiera servir para algo. Con todo, sigo pensando que quizás esto sea lo que necesitamos para resolver ciertos problemas como el de la distribución de los números primos.
La idea no es nueva. He visto una tabla de divisores mínimos para cierto conjunto de números enteros en la famosa colección de tablas de Hoüel (logaritmos decimales, valores naturales de las funciones seno, coseno y tangente, etc.). Lo que hice es agrupar todos los números con un mismo mínimo divisor y formar una estructura de "cociente de un conjunto por una relación de equivalencia"; tan solo que no puedo determinar la relación a partir de los conjuntos.
Como se verá más adelante, elegí un camino inverso al que han seguido la mayoría de los matemáticos profesionales. Todos ellos han buscado un criterio para saber si un número es primo, lo mismo que una función que diera la distribución de todos los primos o, al menos, alguna expresión de grado mayor a la unidad que tuviera una infinidad de números primos, aunque contuviera valores compuestos. En las últimas dos no han tenido ningún éxito, pues no se conoce ninguna fórmula que dé solamente números primos ni tampoco alguna expresión algebraica de la que se esté seguro de que da infinitos valores primos, aunque sea mezclado con algún número de enteros compuestos. En 1932 un matemático indio llamado Sundaram desarrolló una tabla que agrupa a los enteros compuestos. Los primos salen por descarte. También indicó una fórmula que describe algebraicamente a los compuestos y que es la misma que resulta de operar en la forma cuadrática que describo más adelante. Lo expresó como un producto, pero parece que no se dio cuenta de que resultaba en una expresión cuadrática. Yo no sabía de su existencia cuando realicé el trabajo y partí de la forma cuadrática para obtener la tabla, equivalente, pero distinta en su ordenamiento.
Con respecto a criterios de reconocimiento más rápidos y efectivos que el método de la fuerza bruta (dividir un entero por todos los números primos menores a su raíz cuadrada), miles de matemáticos profesionales se han dedicado a buscar y lo que se ha encontrado hasta ahora ayuda un poco pero está lejos de dar una solución práctica al problema.
Por ello se espera que un aficionado no tenga éxito donde los que saben más fracasaron. Pero los aficionados tienen una ventaja sobre los más sabios, que es la falta de prejuicios y de tradiciones. Los profesionales se empeñan en escalar una montaña siempre por la misma ruta, aún sabiendo que todos cayeron en grietas y diferentes trampas. El aficionado no sabe tanto y, por eso mismo, intenta llegar a la cima por cualquier lado, muchas veces ignora por dónde intentaron subir otros. Si lo logra –y no es fácil ni común que lo haga- una vez en ella es muy sencillo determinar qué caminos son imposibles, cuáles los más fáciles y cuáles los difíciles e interesantes como desafío a la virtud del escalador.
Entonces ¿por qué no encontrar una fórmula que dé únicamente todos los números compuestos impares? Como en la criba de Eratóstenes, los primos saldrán por descarte. Para que un número sea compuesto basta, simplemente, con que sea producto de dos factores cualesquiera, cada uno de ellos distinto de la unidad. Esto conduce forzosamente a una ecuación cuadrática en una incógnita o a una forma cuadrática, si el análisis se vuelve de tipo indeterminado.
(Para ver esta tabla más grande y cualquier otra imagen que le resulte pequeña, haga "click" sobre la imagen. Luego vuelva al texto con la flecha izquierda)
BÚSQUEDA DE UN CRITERIO PRÁCTICO PARA DETERMINAR SI UN NÚMERO ES PRIMO O COMPUESTO
Para j perteneciente a Z y k perteneciente a Z, j > 0 y k ≥0,
TEOREMA
Para z número entero positivo, z : primo, z 2
2  no tiene solución en números enteros positivos j > 0 y k ≥ 0.
no tiene solución en números enteros positivos j > 0 y k ≥ 0.
 2
2  no tiene solución en números enteros positivos j > 0 y k ≥ 0.
no tiene solución en números enteros positivos j > 0 y k ≥ 0.
Supongamos que z no es un número primo. Luego existen dos factores ambos mayores que la unidad. Si escribimos z como en el enunciado,  . Ahora bien, 2j + 1 > 1 => j > 0 y 2k + 2j + 1 > 1 => 2k > -2j => k > -j pero, como j debe ser mayor que cero, también k debe ser 0 ó un número mayor. Hemos demostrado no p implica no q, que es lo mismo que demostrar q implica p.
. Ahora bien, 2j + 1 > 1 => j > 0 y 2k + 2j + 1 > 1 => 2k > -2j => k > -j pero, como j debe ser mayor que cero, también k debe ser 0 ó un número mayor. Hemos demostrado no p implica no q, que es lo mismo que demostrar q implica p.
 . Ahora bien, 2j + 1 > 1 => j > 0 y 2k + 2j + 1 > 1 => 2k > -2j => k > -j pero, como j debe ser mayor que cero, también k debe ser 0 ó un número mayor. Hemos demostrado no p implica no q, que es lo mismo que demostrar q implica p.
. Ahora bien, 2j + 1 > 1 => j > 0 y 2k + 2j + 1 > 1 => 2k > -2j => k > -j pero, como j debe ser mayor que cero, también k debe ser 0 ó un número mayor. Hemos demostrado no p implica no q, que es lo mismo que demostrar q implica p.
Si z es primo, luego sus divisores son 1, -1, z y –z. Dado que exigimos para j y k, si existen, que sean positivos, sólo interesan 1 y z.
La factorización de (k+2j+1)² – k² nos conduce forzosamente a una de estas dos igualdades:
2k + 2j + 1 = 1 ó 2j + 1 = 1
2k + 2j + 1 = 1 ó 2j + 1 = 1
La primera es imposible, porque tendríamos k + j = 0 y sabemos que la hipótesis obliga a que ambos sean positivos. La segunda también es imposible porque 2j = 0 => j = 0 y j > 0 por hipótesis. Luego, no existen j y k soluciones de [1], en las condiciones de la hipótesis.
Este teorema garantiza que cualquier número positivo impar que pueda escribirse de esta forma es compuesto. También resultan de ella todos los números compuestos impares positivos, como demostraré a continuación.
Supongamos que existe un número w, entero positivo, impar y compuesto, que no cumple la igualdad w = (2k+2j+1) (2j+1) [*], en las condiciones de la hipótesis. Por ser compuesto, será divisible por un número primo impar p = 2v + 1. Como w es impar, el cociente de w por p también lo será; o sea: w = (2v+1) (2m+1). Ahora bien, hay tres posibilidades: m = v, m > v ó v > m.
Si m = v, w = (2v+1)² , que corresponde al caso k = 0 del teorema demostrado; o sea, que w cumple con [*]; lo que contradice el supuesto.
Si m = v, w = (2v+1)² , que corresponde al caso k = 0 del teorema demostrado; o sea, que w cumple con [*]; lo que contradice el supuesto.
Si m > v, entonces m = v + h; luego: w = (2v+1) (2(v+h)+1) = (2v+1) (2v+2h+1), que también tiene la misma forma del teorema, contradiciendo el supuesto.
Para v > m, tenemos v = m + b; que nos lleva a un resultado análogo. Luego, no existe ningún w entero positivo, impar y compuesto, que no cumpla con el teorema.
La ecuación (2k+2j+1) (2j+1) – p = 0 tiene solución única (en enteros positivos) para p primo, con j = 0. Para p compuesto hay una solución con j = 0 y por lo menos otra con j > 0. Encontrando un algoritmo de cálculo para las soluciones enteras de la ecuación [1], con p entero positivo impar dado, tendríamos un criterio práctico para determinar si un número es primo o no.
Si consideramos la ecuación general de segundo grado con dos incógnitas , la "curva" que describen sus soluciones depende del valor que toma el discriminante
, la "curva" que describen sus soluciones depende del valor que toma el discriminante  . Para el caso que nos ocupa, 4kj + 4j2 + 4j + 2k + 1 – z = 0, el discriminante mayor que cero indica una curva "hiperbólica". En Internet hay una página muy buena del profesor Darío Alejandro Alpern (UTN), en la que se puede utilizar un programa en JAVA para calcular las soluciones enteras. Para los que se interesan más en las fórmulas "elegantes" de los matemáticos teóricos, cualquier ecuación cuadrática en dos incógnitas puede ser llevada, por sustitución de las variables, a la forma
. Para el caso que nos ocupa, 4kj + 4j2 + 4j + 2k + 1 – z = 0, el discriminante mayor que cero indica una curva "hiperbólica". En Internet hay una página muy buena del profesor Darío Alejandro Alpern (UTN), en la que se puede utilizar un programa en JAVA para calcular las soluciones enteras. Para los que se interesan más en las fórmulas "elegantes" de los matemáticos teóricos, cualquier ecuación cuadrática en dos incógnitas puede ser llevada, por sustitución de las variables, a la forma  (con
(con  irracional), que se conoce como ecuación de Pell generalizada. Las soluciones de este tipo de ecuación dependen del desarrollo en fracción continua de la raíz cuadrada de A, pero la bibliografía consultada por mí hasta ahora no trata más que casos particulares. (Ver nota al final)
irracional), que se conoce como ecuación de Pell generalizada. Las soluciones de este tipo de ecuación dependen del desarrollo en fracción continua de la raíz cuadrada de A, pero la bibliografía consultada por mí hasta ahora no trata más que casos particulares. (Ver nota al final)
 , la "curva" que describen sus soluciones depende del valor que toma el discriminante
, la "curva" que describen sus soluciones depende del valor que toma el discriminante  . Para el caso que nos ocupa, 4kj + 4j2 + 4j + 2k + 1 – z = 0, el discriminante mayor que cero indica una curva "hiperbólica". En Internet hay una página muy buena del profesor Darío Alejandro Alpern (UTN), en la que se puede utilizar un programa en JAVA para calcular las soluciones enteras. Para los que se interesan más en las fórmulas "elegantes" de los matemáticos teóricos, cualquier ecuación cuadrática en dos incógnitas puede ser llevada, por sustitución de las variables, a la forma
. Para el caso que nos ocupa, 4kj + 4j2 + 4j + 2k + 1 – z = 0, el discriminante mayor que cero indica una curva "hiperbólica". En Internet hay una página muy buena del profesor Darío Alejandro Alpern (UTN), en la que se puede utilizar un programa en JAVA para calcular las soluciones enteras. Para los que se interesan más en las fórmulas "elegantes" de los matemáticos teóricos, cualquier ecuación cuadrática en dos incógnitas puede ser llevada, por sustitución de las variables, a la forma  (con
(con  irracional), que se conoce como ecuación de Pell generalizada. Las soluciones de este tipo de ecuación dependen del desarrollo en fracción continua de la raíz cuadrada de A, pero la bibliografía consultada por mí hasta ahora no trata más que casos particulares. (Ver nota al final)
irracional), que se conoce como ecuación de Pell generalizada. Las soluciones de este tipo de ecuación dependen del desarrollo en fracción continua de la raíz cuadrada de A, pero la bibliografía consultada por mí hasta ahora no trata más que casos particulares. (Ver nota al final)
Al parecer, una solución para el caso general es complicada, o no hay interés en divulgarla. Yo confieso ser incapaz de dar un método algebraico general de búsqueda de raíces que no sea el de "ensayo y error", pero los profesionales conocen un método universal, por lo que el criterio de determinación planteado más arriba tiene solución práctica y no necesita recurrir a números "astronómicos" como los que suelen aparecer con el teorema de Wilson.
Este tema puede cobrar importancia a partir del revuelo causado por el matemático indio Agrawal, cuando publicó un algoritmo que está siendo perfeccionado por los más importantes matemáticos de las universidades de renombre.
Este algoritmo parece ser más complicado que la obtención de una fracción continua, pero el desarrollo del método que propongo podría destruir la seguridad informática como se practica actualmente, porque habría una manera relativamente rápida de determinar el carácter primo de un número entero muy grande. De todas formas, hay muchas formas de cifrado, como la esteganografía del abate Juan Tritemo y otras que no dependieran de un primo enorme.
Un matemático profesional, que se hace conocer por el pseudónimo Xhantt, me comunicó que, para este tipo de ecuación o forma cuadrática, las soluciones no están todavía acotadas, por lo que por un tiempo largo no podrá usarse ésta como criterio práctico. No puedo discutir con él acerca del tema, porque no estoy capacitado. De todas formas, creo recordar que no solamente se puede recurrir a una ecuación de Pell, sino que esta misma, sin "retocar", tendría un método de resolución debido a Gauss y que desarrolla el número primo o compuesto como fracción continua. El caso general para desarrollar cualquier número como fracción continua, que necesitaría de métodos más refinados, parece que está en un libro del afamado y muy notable matemático soviético Gelfond.
Con todo, lo expuesto aquí basta para mostrar que el problema básico de la divisibilidad o del carácter de primo o compuesto de un número, es, en principio, un problema cuadrático; pues basta con encontrar un par de factores, no importa en cuántos factores primos se divida un número.
Ya que estamos bailando, sigamos haciéndolo mientras tengamos fuerzas y ganas.
La diferencia de cuadrados se divide en dos factores que algunos denominan "quinto caso de factoreo". Se la enseña desde la escuela media y forma parte de un sin fin de demostraciones en teoría de ecuaciones, problemas geométricos y de teoría de números. Es una forma común y cómoda de análisis por la misma sencillez de la descomposición.
Analizando la ecuación cúbica reducida x³ – x – m = 0, se me ocurrió considerar la igualdad x³ – x = m; con lo que, si a es una raíz de la ecuación, a³ – a = m = a (a² – 1).
Según la conocidísima descomposición de una diferencia de cuadrados, a² – 1 = (a + 1) (a – 1). El término independiente se reduce, entonces, al producto de tres factores: a, a + 1 y a – 1. Como el producto de las soluciones resulta ser igual a (-1)^n  y las raíces son tres, procedí a verificar si los términos a + 1 y a – 1 eran raíces, con resultado negativo. Luego dividí la ecuación por x – a, obteniendo una ecuación cuadrática y dos raíces iguales a
y las raíces son tres, procedí a verificar si los términos a + 1 y a – 1 eran raíces, con resultado negativo. Luego dividí la ecuación por x – a, obteniendo una ecuación cuadrática y dos raíces iguales a  y
y  . Nuevamente, el producto de estas dos expresiones es igual a
. Nuevamente, el producto de estas dos expresiones es igual a  , el cociente entre el término independiente y el coeficiente del término cuadrático de la ecuación cuadrática obtenida al dividir por x – a y estas tres sí son las raíces de la ecuación cúbica. Cuando a³ – a es un número entero, es también un número congruente de Fibonacci , para b = 1.
, el cociente entre el término independiente y el coeficiente del término cuadrático de la ecuación cuadrática obtenida al dividir por x – a y estas tres sí son las raíces de la ecuación cúbica. Cuando a³ – a es un número entero, es también un número congruente de Fibonacci , para b = 1.
Desde este punto es sencillo obtener la identidad [*], fácilmente verificable "haciendo las cuentas".
[*], fácilmente verificable "haciendo las cuentas".
 y las raíces son tres, procedí a verificar si los términos a + 1 y a – 1 eran raíces, con resultado negativo. Luego dividí la ecuación por x – a, obteniendo una ecuación cuadrática y dos raíces iguales a
y las raíces son tres, procedí a verificar si los términos a + 1 y a – 1 eran raíces, con resultado negativo. Luego dividí la ecuación por x – a, obteniendo una ecuación cuadrática y dos raíces iguales a  y
y  . Nuevamente, el producto de estas dos expresiones es igual a
. Nuevamente, el producto de estas dos expresiones es igual a  , el cociente entre el término independiente y el coeficiente del término cuadrático de la ecuación cuadrática obtenida al dividir por x – a y estas tres sí son las raíces de la ecuación cúbica. Cuando a³ – a es un número entero, es también un número congruente de Fibonacci , para b = 1.
, el cociente entre el término independiente y el coeficiente del término cuadrático de la ecuación cuadrática obtenida al dividir por x – a y estas tres sí son las raíces de la ecuación cúbica. Cuando a³ – a es un número entero, es también un número congruente de Fibonacci , para b = 1.Desde este punto es sencillo obtener la identidad
 [*], fácilmente verificable "haciendo las cuentas".
[*], fácilmente verificable "haciendo las cuentas".
Esta identidad nos introduce en los racionales de denominador 2, en irracionales cuadráticos de denominadores iguales a potencias de dos y hasta en números complejos con coeficientes irracionales cuadráticos. Sin embargo, también los dos términos de la derecha toman valores enteros cuando dentro de la raíz hay un cuadrado perfecto y la suma del numerador es par. Por lo que esta identidad debería ser tomada en cuenta aún en problemas dentro de Z, que es un dominio de factorización única.
La siguiente y tercera descomposición se obtiene por un camino diferente. Consideremos el triángulo aritmético de Fibonacci:

Si f designa el número de fila del triángulo, f ³ es el valor de la suma de los elementos de la fila, f² – (f – 1) es el primer elemento de la fila y f ²+ (f – 1) el último. El número de sumandos es f.
Conocemos la igualdad 1+2+3+4+5+....+n =
 que se demuestra por inducción matemática en los cursos elementales de álgebra; también sabemos que 1³ + 2³ + 3³ + ...+ n³ =
que se demuestra por inducción matemática en los cursos elementales de álgebra; también sabemos que 1³ + 2³ + 3³ + ...+ n³ =  . Si escribimos la suma anterior hasta el penúltimo sumando, tenemos que:
. Si escribimos la suma anterior hasta el penúltimo sumando, tenemos que:  ; evidentemente:
; evidentemente:
Esta identidad, trivial, podría jugar un papel importante en algunos temas de la Teoría de Números. Es más, cualquier potencia impar cumple la identidad
Como cualquier potencia impar puede ser escrita como una diferencia de cuadrados, es posible aplicar la segunda identidad encontrada a esta fórmula.
Estas dos nuevas expresiones del quinto caso de factoreo son muy elementales y fáciles de comprender. Podrían ser enseñadas sin ninguna dificultad en las escuelas de enseñanza media. Sin embargo, nunca vi una consideración semejante en ninguna parte; lo que me lleva a suponer que estas fórmulas son inéditas. Pregunté a personas con formación matemática terciaria muy superior a la mía si conocían alguna otra descomposición diferente a (a + b) (a – b) para una diferencia de cuadrados y ninguna contestó por la afirmativa; aún aquellas que habían estudiado las extensiones de Kummer.
Ahora veamos cómo obtenemos distintas descomposiciones en diferencias de cuadrados para un mismo número dado que, por simplicidad, tomaremos igual a cuarenta. Esto para no caer en consideraciones teóricas más engorrosas; pero el procedimiento es válido para la generalidad de los números enteros positivos.
40 = 7² – 3²
40 = 11² - 9²
Los valores enteros o racionales de denominador 2 se obtienen de los divisores positivos del número considerado, tomando los pares cuyo producto es igual al número dado y calculando su media aritmética. Al cuadrado de esa media aritmética se le resta el número dado para obtener el segundo cuadrado. Los demás valores surgen al aplicar a cada uno de ellos la segunda fórmula encontrada. El proceso no tiene fin; hay una infinidad de diferencias de cuadrados para un mismo número; ya que la 2ª fórmula encontrada puede ser aplicada recurrentemente. En algunos casos, esta descomposición irracional cuadrática produce valores enteros, además de los irracionales cuadráticos reales o complejos que surgen naturalmente de la fórmula utilizada.
Las expresiones complejas encontradas en la generalidad de los casos podrían resultar factores primos en ciertos anillos de números complejos. Esto pondría a la diferencia de cuadrados dentro de las consideraciones de la teoría algebraica de números y, en especial, de las extensiones de Kummer. Resulta que la fórmula conocida para la descomposición en factores de una diferencia de cuadrados es utilizada en un sinnúmero de demostraciones de teoremas, cálculo de soluciones de ecuaciones diofánticas (como la que surge del Teorema de Pitágoras) y otras consideraciones. Sugiero que esos análisis y demostraciones son incompletos y sus resultados parciales. Una diferencia de cuadrados a² – b² no debe ser considerada a partir de sus componentes a y b, sino desde lo que la diferencia de cuadrados representa como un todo (un número real o complejo).
Pienso que todas las demostraciones en las que aparecen diferencias de cuadrados deben ser profundamente revisadas.
Ahora veamos algo acerca de la ecuación de Pell que, en realidad, fue estudiada por Brouncker y atribuida a Pell por un error de Euler.
Se buscan las soluciones estudiando las unidades en un anillo  porque se descompone la ecuación utilizando el elemental y conocido quinto caso de factoreo; para el cual en este trabajo encontré otra descomposición: la fórmula [*]. ¿Agrega esta nueva forma de re-escritura otro conjunto de soluciones? ¿Son equivalentes estas soluciones? ¿Es por esa razón que todavía no se han acotado debidamente las soluciones?No hay que olvidar que la fórmula [*] conduce también a resultados enteros. O sea, debe tomarse en cuenta para los problemas diofantinos. Para responder a ello, hay que atreverse a desafiar el paradigma dominante y revisar todas las demostraciones considerando estas nuevas identidades y los efectos que provocan. Esto es lo que cabría esperar de alguien que se llame científico; no hay que aceptar las cosas "porque están demostradas", por el temor reverencial hacia personas más inteligentes que la mayoría de nosotros o el peso de la autoridad. Hacer esto significa ser crédulo, no científico. Hacer esto - dirán algunos - es recomenzar continuamente. Sí, pero, ¿no es esto lo que llevó a la Relatividad Restringida? ¿No fue la revisión de la calidad lógica de lo que se conocía desde el Renacimiento lo que pulió la matemática actual y condujo a otras geometrías desconocidas hasta entonces?
porque se descompone la ecuación utilizando el elemental y conocido quinto caso de factoreo; para el cual en este trabajo encontré otra descomposición: la fórmula [*]. ¿Agrega esta nueva forma de re-escritura otro conjunto de soluciones? ¿Son equivalentes estas soluciones? ¿Es por esa razón que todavía no se han acotado debidamente las soluciones?No hay que olvidar que la fórmula [*] conduce también a resultados enteros. O sea, debe tomarse en cuenta para los problemas diofantinos. Para responder a ello, hay que atreverse a desafiar el paradigma dominante y revisar todas las demostraciones considerando estas nuevas identidades y los efectos que provocan. Esto es lo que cabría esperar de alguien que se llame científico; no hay que aceptar las cosas "porque están demostradas", por el temor reverencial hacia personas más inteligentes que la mayoría de nosotros o el peso de la autoridad. Hacer esto significa ser crédulo, no científico. Hacer esto - dirán algunos - es recomenzar continuamente. Sí, pero, ¿no es esto lo que llevó a la Relatividad Restringida? ¿No fue la revisión de la calidad lógica de lo que se conocía desde el Renacimiento lo que pulió la matemática actual y condujo a otras geometrías desconocidas hasta entonces?
 porque se descompone la ecuación utilizando el elemental y conocido quinto caso de factoreo; para el cual en este trabajo encontré otra descomposición: la fórmula [*]. ¿Agrega esta nueva forma de re-escritura otro conjunto de soluciones? ¿Son equivalentes estas soluciones? ¿Es por esa razón que todavía no se han acotado debidamente las soluciones?No hay que olvidar que la fórmula [*] conduce también a resultados enteros. O sea, debe tomarse en cuenta para los problemas diofantinos. Para responder a ello, hay que atreverse a desafiar el paradigma dominante y revisar todas las demostraciones considerando estas nuevas identidades y los efectos que provocan. Esto es lo que cabría esperar de alguien que se llame científico; no hay que aceptar las cosas "porque están demostradas", por el temor reverencial hacia personas más inteligentes que la mayoría de nosotros o el peso de la autoridad. Hacer esto significa ser crédulo, no científico. Hacer esto - dirán algunos - es recomenzar continuamente. Sí, pero, ¿no es esto lo que llevó a la Relatividad Restringida? ¿No fue la revisión de la calidad lógica de lo que se conocía desde el Renacimiento lo que pulió la matemática actual y condujo a otras geometrías desconocidas hasta entonces?
porque se descompone la ecuación utilizando el elemental y conocido quinto caso de factoreo; para el cual en este trabajo encontré otra descomposición: la fórmula [*]. ¿Agrega esta nueva forma de re-escritura otro conjunto de soluciones? ¿Son equivalentes estas soluciones? ¿Es por esa razón que todavía no se han acotado debidamente las soluciones?No hay que olvidar que la fórmula [*] conduce también a resultados enteros. O sea, debe tomarse en cuenta para los problemas diofantinos. Para responder a ello, hay que atreverse a desafiar el paradigma dominante y revisar todas las demostraciones considerando estas nuevas identidades y los efectos que provocan. Esto es lo que cabría esperar de alguien que se llame científico; no hay que aceptar las cosas "porque están demostradas", por el temor reverencial hacia personas más inteligentes que la mayoría de nosotros o el peso de la autoridad. Hacer esto significa ser crédulo, no científico. Hacer esto - dirán algunos - es recomenzar continuamente. Sí, pero, ¿no es esto lo que llevó a la Relatividad Restringida? ¿No fue la revisión de la calidad lógica de lo que se conocía desde el Renacimiento lo que pulió la matemática actual y condujo a otras geometrías desconocidas hasta entonces?
Ciertos autores, como A. O Guelfond, en su libro "Resolución de Ecuaciones en Números Enteros", Editorial Mir, Moscú, 1979, dan métodos para desarrollar algunos tipos de enteros como fracciones continuas. En el caso citado los del tipo A = m² + 1. El mismo autor menciona dos libros en los que hay métodos generales: "Teoría de Números, I. V. Arnold, capítulo VI, Uchpedguiz, 1939 y "Fracciones Continuas", A. Ya. Jinchin, Gostejizdat, M. 1949.



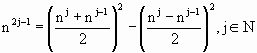


















1 comentario:
Super artykuł. Pozdrawiam serdecznie.
Publicar un comentario