Templos y geometría sagrada

En todos los templos se encierran conceptos que no siempre están al alcance de los concurrentes. Por ejemplo, los templos católicos están casi todos construidos con el altar situado hacia el Este: los fieles marchan desde el ocaso hacia la luz, hacia la salida del Sol, de la muerte a la vida (la catedral de Chartres es una excepción). Pero no es lo único que puede decirse de todo este simbolismo geométrico.

La base o planta de un templo suele estar basada en el doble cuadrado, queriendo decir esto que es un rectángulo que es posible dividir en dos cuadrados.

Esta base, muy frecuente, aparece tanto en templos paganos como de la cristiandad. Otra base común, un poco menos frecuente, es la del triple cuadrado:

Lo primero que vemos es que los ángulos tienen idénticos decimales:

b = c + 45º  y  d = a + 45º

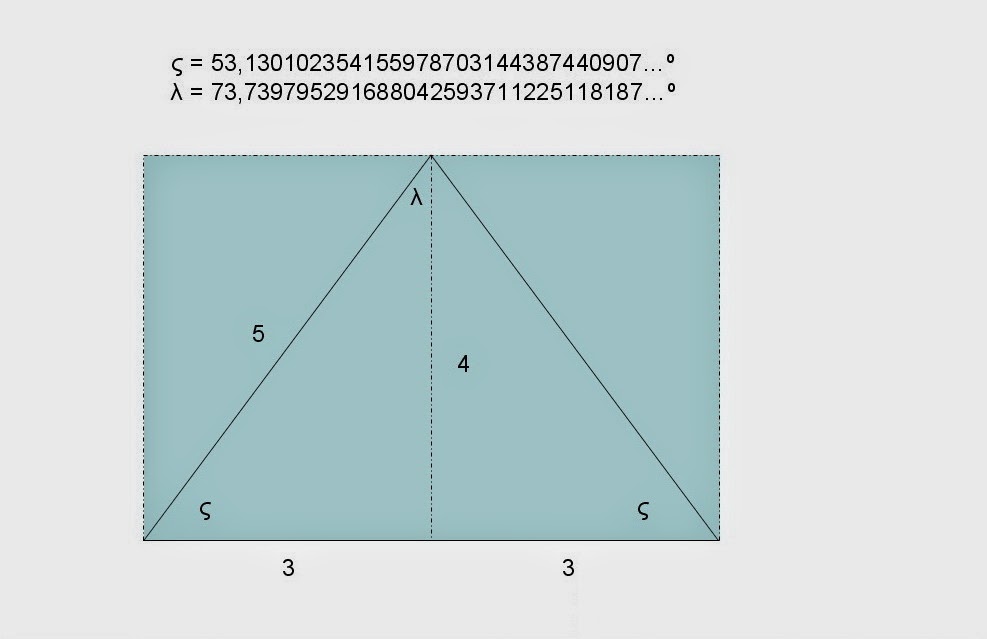
La sorpresa crece cuando consideramos el triángulo sagrado egipcio:

El ángulo "f" es el doble del ángulo "c", del triple cuadrado, y el ángulo "e" es el doble de "a", del doble cuadrado, Estas tres figuras están emparentadas, en la composición arquitectónica hay una unidad temática cuando se usan estas superficies.

Por alguna razón los egipcios consideraban a un número, su duplo, su mitad, su cuadrado y su raíz cuadrada como expresiones de un mismo ente; aunque hay que aclarar que no veían a los números como nosotros, sino como segmentos de rectas.

Insisto: de alguna manera, este triángulo sagrado está emparentado con el doble cuadrado y con el triple cuadrado.

También podemos obtener otros dos triángulos isósceles basados en el triángulo sagrado egipcio: uno con altura proporcional a 4 y base proporcional a 6  y otro con altura proporcional a 3 y base proporcional a 8:

Estas últimas dos son afines (usado en sentido coloquial,  no matemático) , sería un disparate decir que están emparentadas, desde el mismo momento que se forman juntando dos triángulos sagrados.

Viollet-le-Due menciona un "triángulo egipcio", posiblemente derivado del triángulo sagrado, que ha sido utilizado para trazar arcos en aberturas.

Otro triángulo, el triángulo sublime, repite dos ángulos presentes en el doble cuadrado y uno del triángulo sagrado egipcio:

Las figuras emparentadas no terminan con ésta. Podemos observar un ángulo de 63,43...º en el doble cuadrado, que resulta ser el ángulo del vértice superior de la cara plana de la Pirámide de Keops, si consideramos la hipótesis áurea de su construcción.

La semisección de esta cara es un triángulo muy notable, porque vincula los lados de un pentágono, un hexágono y un decágono circunscritos en circunsferencias de radios iguales, constituyendo sus lados una terna pitagórica.

Hay muchos simbolismos encerrados en los templos y correspondencias con acordes musicales, tanto de la escala pitagórica, como de la escala natural, perfecta o de Claudio Ptolomeo; sinfonías geométricas y musicales, cuyas sutilezas no estamos seguros de haber descubierto totalmente.

El misterio de Fermat. Una hipótesis

Pierre de Fermat (Beaumont-de-Lomagne, Francia, 17 de agosto de 1601; Castres, Francia, 12 de enero de 1665) fue una personalidad relevante en la matemática, apodado por Erik Temple Bell (Peterhead, 1883; Watsonville, 1960) "el príncipe de los aficionados".

Llamarlo aficionado podría disminuir ante algunos la importancia de los aportes de este jurista, pues esa era su profesión, que "hacía matemáticas" en sus tiempos de ocio. Sin embargo, se codeó con gigantes como Pascal y Mersenne y se anticipó a los descubrimientos y desarrollos de eminencias como Newton y Descartes.

Tenía la inexplicable conducta de no publicar las demostraciones de sus trabajos aunque, a veces, daba soluciones detalladas y exhaustivas a ciertos problemas, como el de las hipotenusas primas y compuestas de las ternas pitagóricas. Eso es una muestra de que no se trataba, en general, de simples conjeturas, sino que sabía de lo que estaba escribiendo. Hay muy pocos errores en sus conjeturas y una única demostración publicada.

Solía escribir cartas a los matemáticos de su época, en las que planteaba sus problemas como desafíos, a veces con ironías que molestaban a algunos de sus colegas profesionales (Alguien dijo: ¡Condenado francés!). Casi todas sus afirmaciones resultaron correctas y hubo que esperar cien, ciento cincuenta y hasta trescientos cincuenta años para que fueran demostradas por las más encumbradas inteligencias dedicadas a la matemática.

Pero, ¿por qué no publicaba sus trabajos?

Nadie ha podido explicar esto. Ni siquiera habríamos tenido un compendio de sus conjeturas de no ser por el esfuerzo de su hijo Samuel, que las recopiló y las editó como obra póstuma en 1679, en un volumen titulado "Varia opera matemática D. Petri de Fermat: Senatoris Tolosani". Por supuesto, quedaron unas cuantas cartas y anotaciones en los márgenes de los libros que leía.

Yo no tengo una respuesta, pero sí una hipótesis: Fermat pudo haber pertenecido a una sociedad secreta y sus superiores quizás le hayan encargado que sondeara la capacidad de los matemáticos contemporáneos, con fines que no puedo enunciar. En los tiempos de Fermat el conocimiento se hallaba en monasterios y claustros, en universidades y en bibliotecas de nobles y ricos. No pocos de los grandes pertenecieron a alguna clase de clero y otros incursionaron en la alta magia, en la alquimia, en el paganismo y sus mitologías y cosmogonías, en el esoterismo o en las sociedades que se decían depositarias de esos saberes ocultos. Newton, por ejemplo, fue alquimista. Descartes fue rosacruz.

Todos ellos sabían griego y latín y no pocos agregaban hebreo y otras lenguas semíticas. En esas actividades hay dos grandes tipos de experiencias: la enseñanza de doctrinas secretas y las iniciaciones. Una doctrina secreta es un conocimiento que se pasa al recipiente previo juramento de silencio. La iniciación, en cambio, es una experiencia cuya naturaleza es intransmisible. Hay un ritual asociado, que también juran no revelar pero, aunque se violara el secreto del rito, éste por sí mismo no confiere iniciación. Es eficaz solamente en sujetos iniciables.

Siempre se ha dicho, pero no probado, que hay un conocimiento oculto proveniente de una civilización pasada. Quizás los superiores de Fermat quisieron medir cuán cerca se hallaban los profanos de descubrir esos secretos; o bien, de ponderar cuán ocultos estaban todavía.

Lo cierto es que Fermat no publicaba sus demostraciones. Lo demás es conjetura.

Tabla de valores algebraicos de seno y coseno

He aquí una tabla de valores de seno y coseno para ángulos construibles del primer cuadrante y de un número entero de grados sexagesimales, más sus semiángulos.

Para ver el método de cálculo de esta tabla, está el artículo "Como calculé la tabla de valores trigonométricos", del 18/03/2018.

Una gran verdad, que solo comprenden los matemáticos

Encontré en Gaussianos una frase de Lipman Bers que no tiene desperdicio. Estudié Análisis Matemático I con su libro "Cálculus" (si mal no recuerdo, de Columbia University Press), además de otro "Calculus" de Apostol y el enciclopédico tomo I de Rey Pastor. He aquí la joyita:

La del matemático es una profesión extremadamente cruel. Si alguien tiene, digamos, una licenciatura en Químicas, se describirá a sí mismo como un químico. Sin embargo, si alguien lleva siendo profesor de matemáticas durante diez años y le preguntas: “¿Es usted un matemático?”, te contestará “¡Estoy intentando serlo!”

                                                                         Lipman Bers

Esto solo lo comprenden los matemáticos o aquellos que pretenden serlo. También hay una gran similitud con el cristianismo. 

¿Cuánto es 2 + 2? Humor con lección

"¿Cuánto es 2 + 2?"

Parece una pregunta muy simple y clara, de respuesta inequívoca. Veamos cómo responden algunos personajes:

MATEMÁTICO: "Espere, solo unos minutos más, ya he probado que la solución existe y es única, ahora la estoy acotando..."

FILÓSOFO: "¿Qué quiere decir  "2 + 2"?"

TERAPEUTA: "¿Qué quiso decir con "2 + 2"?"

LÓGICO: "Defina mejor "2 + 2" y le responderé."

Más allá de cierta ironía a los vicios y diferentes puntos de vista de los que tienen formaciones profesionales distintas, el lógico y el filósofo no están errados en sus dichos: Todo depende de qué sea "2" y qué "+". La pregunta así formulada es muy vaga, no tiene sentido completo o tiene varias respuestas posibles y excluyentes.

Si "2" es una clase residual de módulo m y "+" denota la suma de clases residuales, 2 + 2 puede ser igual a "1" o a "0". No se asuste, ya le explico.

Primero definamos lo que Gauss llamó "congruencia" y que ahora se conoce como "congruencia de Gauss", porque hay otras congruencias que no son esta a la que me refiero.

Se dice que un número entero "y" es congruente a otro "x" (de módulo m) si (y solo si):
y - x = k.m, donde  k  es un  número entero y m un entero positivo (mayor o igual que 0).
Notación: "y congruente a x, módulo m" suele escribirse: y ≡ x (mod m)

¿Qué tenemos en la definición? Dos números enteros tales que su diferencia es un múltiplo de m.

Pero, escribámoslo de otra manera:

y = k.m + x. Aclaremos con un ejemplo:

19  ≡ 3 (mod 4)  En efecto, 19 - 3 = 4.4, donde k = 4 y m = 4. Aunque, escrito de la segunda manera, deja ver otra cosa:

19 = 4.4 + 3

Si yo divido 19  por 4 el resultado entero es 4 y me sobra un resto igual a 3.

¿A qué llamamos una clase residual de módulo m? A todos los números enteros que dan el mismo resto (o tienen el mismo residuo) al ser divididos por m. Agrupando secuencialmente estos números enteros de igual resto tenemos lo que llamábamos una "escala" en la escuela elemental.

Si nuestra clase residual es el resto "3" de módulo 4, la clase es:

3 = {3, 7, 11, 15, 19, ...}

Es una "escala del 4" a partir de 3. Que significa:

  3 = 0.4 + 3
  7 = 1.4 + 3
11 = 2.4 + 3
15 = 3.4 + 3
19 = 4.4 + 3
y así sucesivamente.

Ahora bien, supongamos que 2 es una clase residual de módulo 4 y que + denota la suma de clases. Esa suma es "0". ¿Por qué?
Porque si tengo un número que dividido por cuatro tiene resto 2 y otro con la misma propiedad, si los sumo, me sobra un 2 por un lado y otro 2 por otro. Luego, esos restos agrupados suman 4 y, por lo tanto el resto es cero. O sea: "sumar dos números con resto 2 de módulo 4 da por resultado un múltiplo de 4, que es lo mismo que decir con resto 0. Veámoslo con símbolos:
z = k.4 + 2; w = q.4 + 2. Si los sumo:

z + w = k.4 + 2 + q.4 + 2

Asociando, conmutando, reagrupando y aplicando propiedad distributiva, tenemos que:

z + w = k.4 + q.4 + 2 + 2 = k.4 + q.4 + 4 = (k+q+1) 4 (Un múltiplo de 4). Luego, el resto es 0.

Así: 2 + 2 = 0 (mod 4)

De forma análoga 2 + 2 = 1 (mod 3)

Broma aparte, la pregunta no tiene sentido completo. Si nos referíamos a números enteros y suma ordinaria, habría que haberlo aclarado; porque no siempre 2 es 2 ni + es más, el más que nosotros conocemos desde niños. Nuestro lógico tenía razón cuando pretendía que definiera mejor lo que significa la pregunta.
Este es un ejemplo de lo que pasa cuando se abusa de la notación. Quizás debiéramos colocar un símbolo por encima de la cifra y cambiarle algo al "+" (como encerrarlo en un círculo); pero la matemática es tan vasta que los símbolos no suelen alcanzar y siempre terminamos repitiendo en alguna parte. La solución es definir bien y aclarar qué significa cada cosa, para que no haya equívocos.

Primalidad

¿Las soluciones enteras de una ecuación como estudio de primalidad?

Tomemos cuatro números enteros positivos: 1, a, b y n; a y b tales que a.b = n. Estos números “a” y “b” pueden ser ambos primos, uno primo y el otro compuesto o los dos compuestos. Si existen a y b cada uno de ellos distinto de la unidad o del valor “n”, n es evidentemente compuesto.

Ahora pongámoslos como raíces de una ecuación en una incógnita:

(x – 1) (x – n) (x – a) (x – b) =

Si generalizamos el problema, podemos hacer al valor determinado “a” una indeterminada “y” y a “b” otra indeterminada “z”. La ecuación en tres indeterminadas queda así:

La ecuación [1] no tiene simultáneamente soluciones enteras x, y, z para n primo.

Dos raíces dobles 1 y n indican el cuadrado de un número primo.

¿Infinitos primos gemelos?

Siguiendo el método del artículo anterior, me permito abordar el problema abierto de la existencia de infinitos pares de primos gemelos. Se llama primos gemelos a dos números primos consecutivos. Por ejemplo: el 5 y el 7 ó 17 y 19. Los únicos primos consecutivos que difieren en una unidad son el 2 y el 3. Como todos los demás son impares, la diferencia será igual a 2.

Como en el caso anterior, planteemos una ecuación cuadrática, en principio, en una variable:

x² - bx + c = 0

Sea c igual al producto de dos primos gemelos. Luego, c = p (p + 2) = p² + 2p

Si queremos que p y p + 2 sean raíces de la ecuación, b debe ser igual a: p + p + 2 = 2p + 2.

Reemplacemos en la ecuación original:

x² - (2p + 2)x + p² + 2p = 0

En este caso p no es una variable, sino que es un valor determinado primo impar. Si quisiéramos investigar a la totalidad de los números primos impares, deberíamos convertir a p en una variable "y". Hagámoslo.

x² - (2y + 2)x + y² + 2y = 0

Haciendo las operaciones y reordenando, tenemos:

x² - 2yx - 2x + 2y + y² = 0

Si se pudiera determinar la cantidad de soluciones enteras para esta ecuación diofántica cuadrática en dos variables, se podría resolver el problema de la potencia del conjunto de los primos gemelos. Es más: si las raíces de esta ecuación están acotadas, se podría llegar a obtener soluciones concretas; es decir, pares de primos gemelos de cualquier magnitud humanamente manejable.

Sin embargo, "y" no siempre representará a un número primo; esta ecuación también puede tener soluciones enteras compuestas impares consecutivas.  Los pares de primos gemelos serán un subconjunto de esas soluciones. Los primos gemelos sumados dan un número par divisible por 12. Esto es inmediato: la suma de dos números impares es par; también es el doble de la media aritmética de esos dos primos, que no es otra cosa que el número par que los separa; que, a su vez, es divisible por 3, puesto que es el único compuesto entre tres números enteros consecutivos.

A priori, uno podría suponer que la ecuación es una cónica. Pero resulta ser una forma degenerada. Resulta ser dos rectas paralelas de pendiente unitaria, una de ellas x = y y la otra x - 2 = y. Hay infinitas soluciones, pero su forma no aporta nada al tema.

La conjetura fuerte de Goldbach

Hardy lo calificó como el problemas más difícil, no solamente de la teoría de números sino, de toda la matemática.

No soy quien para desautorizar a Hardy. Apenas un aficionado mediocre o peor.

Sin embargo, a veces la dificultad disminuye si se encuentra una manera de enunciar el problema que lo lleve a un terreno menos escabroso.

La conjetura dice que todo número entero positivo par mayor que 4 es expresable como suma de dos números primos impares, pudiendo repetirse un mismo número primo.

Se me ocurre que está suficientemente estudiado el caso de las ecuaciones cuadráticas diofánticas (o diofantinas). Si no exhaustiva o cabalmente, por lo menos en grado suficiente.

Sea una ecuación cuadrática en una variable x² -bx + c = 0. b es un número entero par mayor que 4, si y solo si existe por lo menos un entero positivo c tal que la ecuación tiene dos raíces enteras impares mayores o iguales que 3.

Yo diría que esto mismo puede ser un buen camino para demostrarlo. En teoría de ecuaciones hace mucho que se sabe que el entero c es igual al producto de las raíces y que el entero b es la suma de esas raíces. También, el teorema general de la aritmética garantiza que hay una infinidad de enteros impares tales que son producto de dos números primos impares, cualesquiera sean estos primos. Y la suma de dos números impares es un número par. Si no está claro que todo par es un "b" generado por la suma de dos primos que factorean un "c", habría que suponer que hay un b que no es generado por un c en esas condiciones y llegar a un absurdo. Planteado el problema como una ecuación cuadrática, tenemos a mano la teoría de Galois y todo lo que se sabe de ecuaciones cuadráticas en una y dos variables.