Templos y geometría sagrada

En todos los templos se encierran conceptos que no siempre están al alcance de los concurrentes. Por ejemplo, los templos católicos están casi todos construidos con el altar situado hacia el Este: los fieles marchan desde el ocaso hacia la luz, hacia la salida del Sol, de la muerte a la vida (la catedral de Chartres es una excepción). Pero no es lo único que puede decirse de todo este simbolismo geométrico.

La base o planta de un templo suele estar basada en el doble cuadrado, queriendo decir esto que es un rectángulo que es posible dividir en dos cuadrados.

Esta base, muy frecuente, aparece tanto en templos paganos como de la cristiandad. Otra base común, un poco menos frecuente, es la del triple cuadrado:

Lo primero que vemos es que los ángulos tienen idénticos decimales:

b = c + 45º  y  d = a + 45º

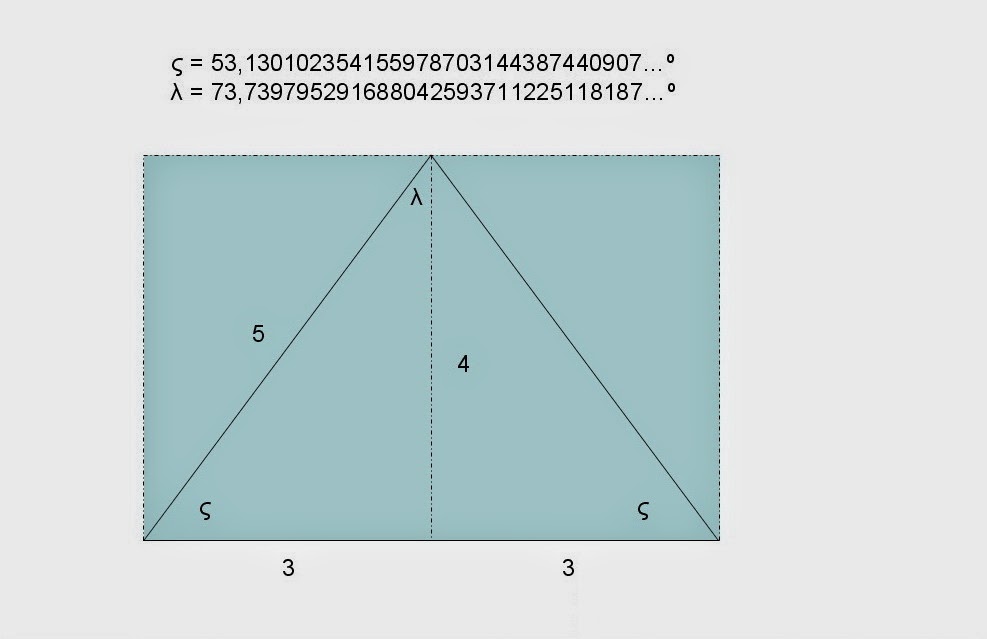
La sorpresa crece cuando consideramos el triángulo sagrado egipcio:

El ángulo "f" es el doble del ángulo "c", del triple cuadrado, y el ángulo "e" es el doble de "a", del doble cuadrado, Estas tres figuras están emparentadas, en la composición arquitectónica hay una unidad temática cuando se usan estas superficies.

Por alguna razón los egipcios consideraban a un número, su duplo, su mitad, su cuadrado y su raíz cuadrada como expresiones de un mismo ente; aunque hay que aclarar que no veían a los números como nosotros, sino como segmentos de rectas.

Insisto: de alguna manera, este triángulo sagrado está emparentado con el doble cuadrado y con el triple cuadrado.

También podemos obtener otros dos triángulos isósceles basados en el triángulo sagrado egipcio: uno con altura proporcional a 4 y base proporcional a 6  y otro con altura proporcional a 3 y base proporcional a 8:

Estas últimas dos son afines (usado en sentido coloquial,  no matemático) , sería un disparate decir que están emparentadas, desde el mismo momento que se forman juntando dos triángulos sagrados.

Viollet-le-Due menciona un "triángulo egipcio", posiblemente derivado del triángulo sagrado, que ha sido utilizado para trazar arcos en aberturas.

Otro triángulo, el triángulo sublime, repite dos ángulos presentes en el doble cuadrado y uno del triángulo sagrado egipcio:

Las figuras emparentadas no terminan con ésta. Podemos observar un ángulo de 63,43...º en el doble cuadrado, que resulta ser el ángulo del vértice superior de la cara plana de la Pirámide de Keops, si consideramos la hipótesis áurea de su construcción.

La semisección de esta cara es un triángulo muy notable, porque vincula los lados de un pentágono, un hexágono y un decágono circunscritos en circunsferencias de radios iguales, constituyendo sus lados una terna pitagórica.

Hay muchos simbolismos encerrados en los templos y correspondencias con acordes musicales, tanto de la escala pitagórica, como de la escala natural, perfecta o de Claudio Ptolomeo; sinfonías geométricas y musicales, cuyas sutilezas no estamos seguros de haber descubierto totalmente.