Los egipcios tenían la costumbre de escribir cualquier fracción 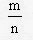 como una suma de
fracciones de numeradores unitarios con denominadores distintos y,
eventualmente, un entero, para el caso de fracciones impropias. Algunos autores
han dicho que esta manera algo extraña de escribir fracciones, les daba un
método rápido y casi “visual” de comparar quebrados, que no demandaba expresar
numéricamente el resultado del cociente para saber si una fracción era mayor ,
igual o menor que otra:
como una suma de
fracciones de numeradores unitarios con denominadores distintos y,
eventualmente, un entero, para el caso de fracciones impropias. Algunos autores
han dicho que esta manera algo extraña de escribir fracciones, les daba un
método rápido y casi “visual” de comparar quebrados, que no demandaba expresar
numéricamente el resultado del cociente para saber si una fracción era mayor ,
igual o menor que otra:
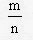 como una suma de
fracciones de numeradores unitarios con denominadores distintos y,
eventualmente, un entero, para el caso de fracciones impropias. Algunos autores
han dicho que esta manera algo extraña de escribir fracciones, les daba un
método rápido y casi “visual” de comparar quebrados, que no demandaba expresar
numéricamente el resultado del cociente para saber si una fracción era mayor ,
igual o menor que otra:
como una suma de
fracciones de numeradores unitarios con denominadores distintos y,
eventualmente, un entero, para el caso de fracciones impropias. Algunos autores
han dicho que esta manera algo extraña de escribir fracciones, les daba un
método rápido y casi “visual” de comparar quebrados, que no demandaba expresar
numéricamente el resultado del cociente para saber si una fracción era mayor ,
igual o menor que otra:
Sin embargo, no es necesario hacer divisiones para comparar
fracciones. Todos aprendimos en la escuela elemental que se cumplen estas tres
propiedades:
Pero es cierto que no puede darse la magnitud de la diferencia con
rapidez, por este método, sin hacer algún otro cálculo. De todas formas, el
egipcio común utilizaba tablas de descomposición de fracciones, tal como
nosotros usamos alguna vez las tablas de logaritmos; y no sabemos de qué manera
lograban las descomposiciones aquellos que construían esas tablas. De esta
forma, la pregunta acerca de cuál era la
ventaja –si la había- para utilizar este particular modo de escritura,
queda pendiente de respuesta.
Hay, por lo menos cuatro papiros matemáticos egipcios. Yo no tengo
instrucción en ninguna de las tres formas de escritura egipcia; pero recuerdo
haber leído la opinión de un experto acerca de uno muy famoso, escrito por un
tal Ahmes o Ahmesu (las transliteraciones cambian con los autores). Este
experto decía que, a juzgar por algunos errores groseros cometidos, Ahmes era
un simple copista que no entendía lo que estaba copiando y que, con seguridad,
la aritmética egipcia era varios siglos anterior a ese papiro. Los papiros
encontrados hasta hoy tratan temas prácticos y elementales, como para capacitar
mano de obra. Los egiptólogos profesionales siguen la tendencia “orgullosa” de
atribuir a los antiguos en general incipientes e ingenuos conocimientos,
cargados de superstición y livianos de sabiduría. Refuerzan su postura con la
escasez y elementalidad de los manuscritos encontrados (prueba empírica); pero
no reparan en que la Gran Pirámide está mejor orientada que el Observatorio de
París y que el encuadre de la base de 232,8 m es extraordinariamente preciso y
difícilmente practicable hoy, con nuestras mejores técnicas. Por eso se alzarán
voces en contra de lo que voy a sugerir ahora; aunque de ninguna manera digo
que ellos supieran lo mismo que nosotros. Quizás ni sospechemos las razones de
su método, pero hay algo detrás de ello, sin lugar a dudas.
Donde parece haber una ventaja significativa es en la resolución de
ecuaciones diofantinas de segundo, tercero y otros grados.
En cualquier ecuación  , las raíces
, las raíces  cumplen:
cumplen: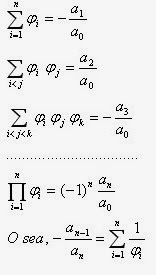
 , las raíces
, las raíces  cumplen:
cumplen: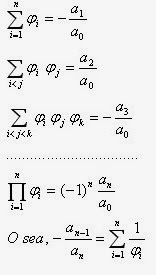
Ahora bien,  es la n-sima parte de la media armónica de los valores de las raíces. De esto se desprende que este cociente es una cota inferior de la menor raíz de cualquier ecuación cuya expresión sea un polinomio de grado arbitrario n.
es la n-sima parte de la media armónica de los valores de las raíces. De esto se desprende que este cociente es una cota inferior de la menor raíz de cualquier ecuación cuya expresión sea un polinomio de grado arbitrario n.
 es la n-sima parte de la media armónica de los valores de las raíces. De esto se desprende que este cociente es una cota inferior de la menor raíz de cualquier ecuación cuya expresión sea un polinomio de grado arbitrario n.
es la n-sima parte de la media armónica de los valores de las raíces. De esto se desprende que este cociente es una cota inferior de la menor raíz de cualquier ecuación cuya expresión sea un polinomio de grado arbitrario n.
Si por un algoritmo pudiera descomponerse el cociente de los
coeficientes an-1 y an en suma de fracciones unitarias,
tendríamos una manera de obtener las raíces de la ecuación. Como esta
descomposición por lo general no es única, habría que hacer una discusión de
las soluciones. Otra posibilidad muy interesante surge del hecho de que si se
halla una descomposición de m factores, pueden encontrarse infinitas
descomposiciones de n factores, n > m. En general, para cualquier n esta
descomposición no es única; así es que pueden ser planteadas otras ecuaciones
del mismo grado y superiores con una raíz común.
Si bien el método egipcio parece ser aplicable solamente a
fracciones con denominadores enteros, no descarto que sea posible extender el
algoritmo al cálculo de denominadores algebraicos explícitos. Si esto es
cierto, toda ecuación con raíces algebraicas explícitas podría ser resuelta por
este método.
También es destacable que la divisibilidad de un entero q está muy
relacionada con el desarrollo de  como fracción
decimal, según demostró Pascal y desarrollaron posteriormente John Wallis, Jean
Bernoulli, Euler y Lambert.
como fracción
decimal, según demostró Pascal y desarrollaron posteriormente John Wallis, Jean
Bernoulli, Euler y Lambert.
 como fracción
decimal, según demostró Pascal y desarrollaron posteriormente John Wallis, Jean
Bernoulli, Euler y Lambert.
como fracción
decimal, según demostró Pascal y desarrollaron posteriormente John Wallis, Jean
Bernoulli, Euler y Lambert.
La resolución de ecuaciones de cualquier grado está íntimamente
ligada a la divisibilidad del cociente del coeficiente independiente por el
coeficiente del término de mayor grado.
Hay un hecho sin explicación racional de parte de nuestra ciencia:
los egipcios no descomponían la fracción  , la utilizaban así, directamente como se escribe, mientras
que la descomposición es posible:
, la utilizaban así, directamente como se escribe, mientras
que la descomposición es posible: 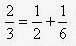 . Tampoco hacían nada con
. Tampoco hacían nada con 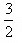 , el famoso “sesqui” de los latinos, que formaba parte de la
versión racional del triángulo sagrado egipcio
, el famoso “sesqui” de los latinos, que formaba parte de la
versión racional del triángulo sagrado egipcio  , cuya duplicación es el triángulo sagrado egipcio entero
primitivo (lados primos entre sí): (3, 4, 5). Se desconoce el por qué de la
denominación “sagrado”, pero tiene algo que ver con el concepto de “sesqui”
(una vez y media).
, cuya duplicación es el triángulo sagrado egipcio entero
primitivo (lados primos entre sí): (3, 4, 5). Se desconoce el por qué de la
denominación “sagrado”, pero tiene algo que ver con el concepto de “sesqui”
(una vez y media).
 , la utilizaban así, directamente como se escribe, mientras
que la descomposición es posible:
, la utilizaban así, directamente como se escribe, mientras
que la descomposición es posible: 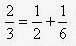 . Tampoco hacían nada con
. Tampoco hacían nada con 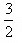 , el famoso “sesqui” de los latinos, que formaba parte de la
versión racional del triángulo sagrado egipcio
, el famoso “sesqui” de los latinos, que formaba parte de la
versión racional del triángulo sagrado egipcio  , cuya duplicación es el triángulo sagrado egipcio entero
primitivo (lados primos entre sí): (3, 4, 5). Se desconoce el por qué de la
denominación “sagrado”, pero tiene algo que ver con el concepto de “sesqui”
(una vez y media).
, cuya duplicación es el triángulo sagrado egipcio entero
primitivo (lados primos entre sí): (3, 4, 5). Se desconoce el por qué de la
denominación “sagrado”, pero tiene algo que ver con el concepto de “sesqui”
(una vez y media).


No hay comentarios:
Publicar un comentario